Answer:
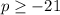
Explanation:
1. Simplify the expression
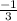 ·
·
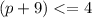
Multiply the fractions:
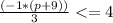
Expand the parentheses:
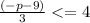
Break up the fraction:
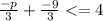
Find the greatest common factor of the numerator and denominator:

Factor out and cancel the greatest common factor:
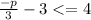
2. Group all constants on the right side of the inequality
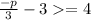
Add 3 to both sides:
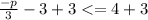
Simplify the arithmetic:
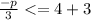
Simplify the arithmetic:
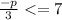
3. Isolate the p
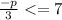
Multiply to both sides by 3:
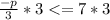
Group like terms:
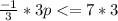
Simplify the left side:
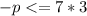
Simplify the arithmetic:

4. Isolate the p

Multiply both sides by-1:
When dividing or multiplying by a negative number, always flip the inequality sign:
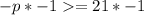
Remove the one(s):
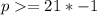
Simplify the arithmetic:
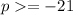
5. Solution on a coordinate plane
Solution:
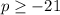
Interval notation:
![[-21, { \infty} ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/mrvr09q96pm3bhrcmtzbe3ls4rnct6rrbb.png)
Terms and Topics:
Linear Equalities