Question

Plzzzz help i need help really baddd

Answer 1

`sin(B)=0.6`

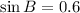
Explanation:

We remember that the sine of any angle in a right triangle is the side opposite that angle divided by the hypotenuse. So,
`sin(B)=(CD)/(BD)=(CD)/(√(69))`.

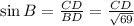But we don't know CD!

Aha! We can use the pythagorean theorem! Because
`\triangle BCD` is right, we have that
`BC^2+CD^2=BD^2`, so
`44+CD^2=69`.

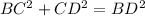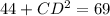Solving gives
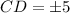`CD=\pm 5`. However, because CD is a side length, it must be positive. So, we have
`CD=5`.

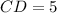Plugging into our formula for
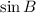`sin(B)` gives
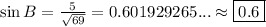`sin(B)=(5)/(√(69))=0.601929265...\approx \boxed{0.6}` rounded to the nearest hundredth.

Note: Find
`cos(D)`. Note that(if you've done it correctly) it equals
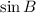`sin(B)`. Coincidence? If not, try and prove it!

Hint for note: It's not a coincidence. One of the first facts you'll learn is that
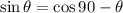`sin(\theta)=cos(90-\theta)`. Try and prove this for acute angles in a triangle!