Explanation:

Given that
A line segment AB having coordinates of A as (1, - 5) and coordinates of B as (- 4, 5).
Let assume that x - axis divides the line segment joining the points A (1, - 5) and B (- 4, 5) in the ratio k : 1 at C.
Let assume that coordinates of C be (x, 0).
We know,
Section formula :-
Let P(x₁, y₁) and Q(x₂, y₂) be two points in the coordinate plane and R(x, y) be the point which divides PQ internally in the ratio m₁ : m₂. Then, the coordinates of R will be:
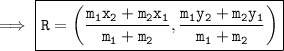
So, on substituting the values, we get
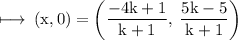
On comparing y - coordinate on both sides, we get
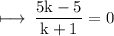
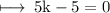
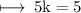
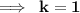
Hence,
The x - axis divides the line segment joining the points A (1, - 5) and B (- 4, 5) in the ratio 1 : 1 at C.
Now, On comparing x - coordinate on both sides, we get
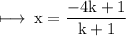
On substituting the value of k, we get
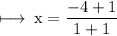
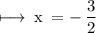
Hence,
The coordinates of point of intersection, C is
