Question

The magnitude of the electrostatic force between two point charges Q and q of the same sign is given by F(x) = KQq/x², where x is the distance between the charges and K = 9 × 10⁹ N•m²/C² is a physical constant ( C stands for Coulomb, the unit of charge & N stands for Newton, the unit of force ).

A.) Find the instantaneous rate of change of the force with respect to the distance between the charges.
B.) For two identical charges with Q = q = 2C, what is the instantaneous rate of change of the force at a separation of x = 0.001m ?

​

Answer 1

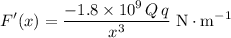`\displaystyle F^(\prime)(x) = (-1.8 * 10^(9)\, Q \, q)/(x^(3))\; \rm N\cdot m^(-1)` assuming that the units of
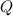`Q` and
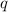`q` are both coulomb.

If
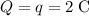`Q = q = 2\; \rm C`, then
`F^(\prime)(0.001\; \rm m) = -7.20* 10^(19)\; \rm N \cdot m^(-1)`.

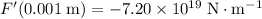Step-by-step explanation:

It is given that:

`\displaystyle F(x) = (k \cdot Q \cdot q)/(x^(2))`.

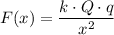Equivalently:

`\displaystyle F(x) = k \cdot Q \cdot q \cdot x^(-2)`.

Differentiate
`F(x)` with respect to
`x` to find the corresponding instantaneous rate of change.

By the power rule for derivatives,
`\begin{aligned} (d)/(dx)\, \left[x^(-2)\right] &= (-2)\, x^(-3) \end{aligned}`.

Likewise, when differentiating
`F(x)`:

`\begin{aligned}F^(\prime)(x) &= (d)/(dx)\left[k\cdot Q \cdot q \cdot x^(-2)\right] \\ &= k \cdot Q \cdot q \cdot (d)/(dx) \left[x^(-2)\right] \\ &= (-2)\, k \cdot Q \cdot q \cdot x^(-3) \\ &= ((-2)\, k \cdot Q \cdot q)/(x^(3))\end{aligned}`.

It is given that
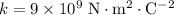`k = 9 * 10^(9)\; \rm N \cdot m^(2) \cdot C^(-2)`. Assume that the units of
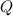`Q` and
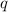`q` are both coulomb, and that the unit of
`x` is meter (such that no unit conversion would be necessary,) substitute the value of
`k` into the expression for
`F^(\prime)(x)`:

`\begin{aligned} F^(\prime)(x) &= ((-2)\, k \cdot Q \cdot q)/(x^(3)) \\ &= \frac{(-2) * 9 * 10^(9)\; {\rm N \cdot m^(2) \cdot C^(-2)} \cdot (Q\; {\rm C}) \cdot (q \; {\rm C})}{({x\;\rm m})^(3)} \\ &= (1.8 * 10^(10)\, Q \cdot q)/(x^(3))\; \rm N \cdot m^(-1)\end{aligned}`.

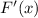Substitute in
`Q = 2`,
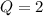`q = 2`, and
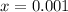`x = 0.001` into the expression and evaluate:

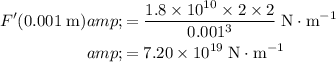`\begin{aligned}F^(\prime)({0.001\; \rm m}) &= (1.8 * 10^(10)* 2 * 2)/(0.001^(3))\; \rm N \cdot m^(-1) \\ &= 7.20 * 10^(19)\; \rm N \cdot m^(-1) \end{aligned}`.