Answer:
Calculate the area of the sector and the area of the rectangle separately, then add them together to determine the area of the composite figure.
Rectangle
Area of a rectangle = width × length
= 4 × 5.5
= 22 m²
Sector
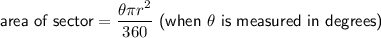
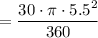
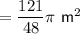
Total area
total area = area of rectangle + area of sector

= 29.91943148...
= 29.9 m² (nearest tenth)