Question

Can someone please help me with #13-17?Please,I really need the help.I have been stuck on this for 1 hour and still don't know what to do.​

Answer 1

Problem 13

The domain is the set of allowed x inputs. Locate the left-most point. From there, draw a vertical line until you reach the x axis. You should reach x = -3. This is the smallest x value in the domain, and it is included due to the closed circle here. We cannot repeat this for the right-most point because there is no right-most point. The arrow shows the curve goes on forever to the right. So infinity is the largest x value.

In short, x is between -3 and infinity and we write it like so:
`-3 \le x < \infty`

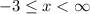
You could write it also as
`-3 \le x` or
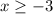`x \ge -3`, but the first notation mentioned with infinity seems to be the most descriptive in my opinion. That first notation also can be readily converted to the interval notation
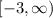`[-3, \infty)`. The square bracket says "include -3" while the curved parenthesis says we exclude infinity. We can never reach infinity, so there's no way to include it. It's not a number. It's a concept.

As for the range, we will do the same idea as before. This time we'll look to the y axis. The highest we can go is y = 3 and we can't actually reach this value due to the open hole here. There is no smallest y value because of the arrow on the curve pointing downward forever.

Therefore, the range is the set of y values between negative infinity and 3, excluding both endpoints. We would say
`-\infty < y < 3`

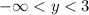
Now to the question whether this is a function or not. We can use the vertical line test to check. If it is possible to draw a single vertical line through more than one point on the curve, then we do not have a function. We can see that such a thing would happen for this curve. For instance, draw a vertical line through x = 0 (aka the y axis itself) and we see that two points are on the curve at the same time here. The input x = 0 leads to more than one output. This is one example of infinitely many to see why we do not have a function.

---------------------------

Answers:

• Domain:
  `-3 \le x < \infty`
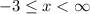
• Range:
  `-\infty < y < 3`
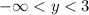
• Function: No

===========================================================

Problem 14

The inputs x span from x = -4 to x = 3, excluding both endpoints due to the open holes. They can be thought of as potholes on the road you don't want to drive on (simply because that portion of the road doesn't even exist).

Therefore, the domain is
`-4 < x < 3`

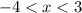
The range is
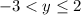`-3 < y \le 2` because the lowest y can get is y = -3 and the highest it can get is y = 2. However, we exclude y = -3 itself because of the open hole. We include y = 2.

In contrast to problem 13, we have a function this time. It is impossible to draw a single straight vertical line through more than one point on this V shape curve. This graph passes the vertical line test.

---------------------------

Answers:

• Domain:
  `-4 < x < 3`
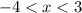
• Range:
  `-3 < y \le 2`
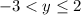
• Function: Yes

===========================================================

Problem 15

The left-most point occurs when x = -5 and the right-most point is when x = 4. We include both endpoints since there are no open holes here. Every bit of road is defined. The domain is
`-5 \le x \le 4`

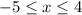
Locate any of the many lowest valley points. Draw a horizontal line until you reach the y axis. You should reach y = -3. Repeat for one of the highest points and you'll get to y = 3. The range is
`-3 \le y \le 3`

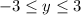
Like problem 14, this graph passes the vertical line test. Therefore, we have a function. Any x input, in the domain mentioned, produces exactly one and only one y output. The key here is "in the domain mentioned". We cannot plug in x values outside this domain.

---------------------------

Answers:

• Domain:
  `-5 \le x \le 4`
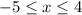
• Range:
  `-3 \le y \le 3`
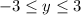
• Function: Yes

===========================================================

Problem 16

There's not much different from something like problem 14. The domain here is
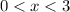`0 < x < 3` and the range is
`2 < y < 4`

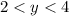
We have a function because this graph passes the vertical line test.

---------------------------

Answers:

• Domain:
  `0 < x < 3`
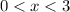
• Range:
  `2 < y < 4`
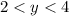
• Function: Yes

===========================================================

Problem 17

Same idea as before. The left-most point occurs when x = 0 and the right-most point is when x = 6. Therefore
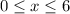`0 \le x \le 6` is our domain here.

The highest point seems to occur at y = 18 based on what the graph says. The lowest point is perhaps when y = -9. These two y values are estimations. So it's possible the range is
`-9 \le y \le 18`

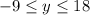
We have another function here because this curve passes the vertical line test. Only problems 12 and 13 were a non-function. Everything else is a function.

---------------------------

Answers:

• Domain:
  `0 \le x \le 6`
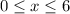
• Range:
  `-9 \le y \le 18`
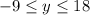
• Function: Yes