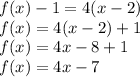Answer:
The equation of a tangent line is y = 4x-7
Explanation:
We are given our quadratic function:-
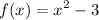
Since we want to find a line that is tangent to the parabola, let's recall our basic differential.
Differential (Power/Exponent)
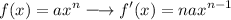
Differential (Constant)
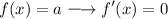
For a = constant.
First, differentiate the function.
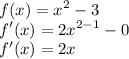
Then substitute x = 2 in f'(x) to find the slope at x = 2 for parabola.
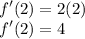
Therefore, slope at x = 2 is 4.
Form a point-slope equation:-
Point-Slope (Derivative)
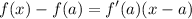
Let a = x = 2
To find f(a), substitute x = a = 2 in x^2-3.
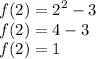
Therefore our f(a) is 1.
We know:-
Therefore the tangent equation is:-