Answer:
To find out whether a fraction will have a terminating or recurring decimal, look at the prime factors of the denominator when the fraction is in its most simple form. If they are made up of 2s and/or 5s, the decimal will terminate. If the prime factors of the denominator contain any other numbers, the decimal will recur.
Some decimals are irrational, which means that the decimals go on forever but not in a pattern (they are not recurring). An example of this would be pi or
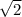 .
.
Explanation: