Question

A) Evaluate the limit using the appropriate properties of limits. (If an answer does not exist, enter DNE.)

lim x→[infinity]

2x2 − 5

7x2 + x − 3

B) Find the limit, if it exists. (If an answer does not exist, enter DNE.)

lim x → [infinity]

5x − 3

2x + 1

C) Find the limit, if it exists. (If an answer does not exist, enter DNE.)

lim x → −[infinity]

x − 1

x2 + 8

D) Find the limit, if it exists. (If an answer does not exist, enter DNE.)

lim t → [infinity]

sqrt1a.gif t+ t2

3t − t2

E) Find the limit, if it exists. (If an answer does not exist, enter DNE.)

lim x → [infinity]

x4

sqrt1a.gif x8 + 9

F) Find the limit, if it exists. (If an answer does not exist, enter DNE.)

lim x→[infinity]

sqrt2a.gif x + 5x2

3x − 1

G) Find the limit, if it exists. (If an answer does not exist, enter DNE.)

lim x → [infinity]

x4 − 2x

Answer 1

For purely rational functions, the general strategy is to compare the degrees of the numerator and denominator.

A)

`\displaystyle \lim_(x\to\infty) (2x^2-5)/(7x^2+x-3) = \boxed{\frac27}`

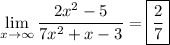
because both numerator and denominator have the same degree (2), so their end behaviors are similar enough that the ratio of their coefficients determine the limit at infinity.

More precisely, we can divide through the expression uniformly by x ²,

`\displaystyle \lim_(x\to\infty) (2x^2-5)/(7x^2+x-3) = \lim_(x\to\infty) \frac{2-\frac5{x^2}}{7+\frac1x-\frac3{x^2}}`

Then each remaining rational term converges to 0 as x gets arbitrarily large, leaving 2 in the numerator and 7 in the denominator.

B) By the same reasoning,

`\displaystyle \lim_(x\to\infty) (5x-3)/(2x+1) = \boxed{\frac52}`

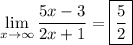
C) This time, the degree of the denominator exceeds the degree of the numerator, so it grows faster than x - 1. Dividing a number by a larger number makes for a smaller number. This means the limit will be 0:

`\displaystyle \lim_(x\to-\infty) (x-1)/(x^2+8) = \boxed{0}`

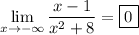
More precisely,

`\displaystyle \lim_(x\to-\infty) (x-1)/(x^2+8) = \lim_(x\to-\infty)\frac{\frac1x-\frac1{x^2}}{1+\frac8{x^2}} = \frac01 = 0`

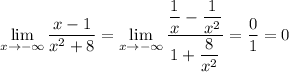
D) Looks like this limit should read

`\displaystyle \lim_(t\to\infty)(√(t)+t^2)/(3t-t^2)`

which is just another case of (A) and (B); the limit would be

`\displaystyle \lim_(t\to\infty)(√(t)+t^2)/(3t-t^2) = -1`

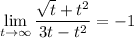
That is,

`\displaystyle \lim_(t\to\infty)(√(t)+t^2)/(3t-t^2) = \lim_(t\to\infty)\frac{\frac1{t^(3/2)}+1}{\frac3t-1} = \frac1{-1} = -1`

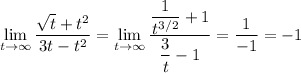
However, in case you meant something else, such as

`\displaystyle \lim_(t\to\infty)(√(t+t^2))/(3t-t^2)`

then the limit would be different:

`\displaystyle \lim_(t\to\infty)(√(t^2)√(\frac1t+1))/(3t-t^2) = \lim_(t\to\infty)(t√(\frac1t+1))/(3t-t^2) = \lim_(t\to\infty)(√(\frac1t+1))/(3-t) = 0`

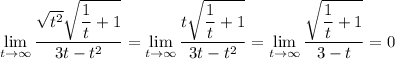
since the degree of the denominator is larger.

One important detail glossed over here is that

`√(t^2) = |t|`

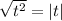
for all real t. But since t is approaching *positive* infinity, we have t > 0, for which |t | = t.

E) Similar to (D) - bear in mind this has the same ambiguity I mentioned above, but in this case the limit's value is unaffected -

`\displaystyle \lim_(x\to\infty) (x^4)/(√(x^8+9)) = \lim_(x\to\infty)\frac{x^4}{√(x^8)\sqrt{1+\frac9{x^8}}} = \lim_(x\to\infty)\frac{x^4}{x^4\sqrt{1+\frac9{x^8}}} = \lim_(x\to\infty)\frac1{\sqrt{1+\frac9{x^8}}} = \boxed{1}`

Again,

`√(x^8) = |x^4|`

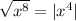
but x ⁴ is non-negative for real x.

F) Also somewhat ambiguous:

`\displaystyle \lim_(x\to\infty)(√(x+5x^2))/(3x-1) = \lim_(x\to\infty)(√(x^2)√(\frac1x+5))/(3x-1) = \lim_(x\to\infty)(x√(\frac1x+5))/(3x-1) = \lim_(x\to\infty)(√(\frac1x+5))/(3-\frac1x) = \frac{\sqrt5}3`

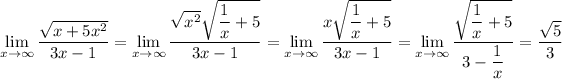
or

`\displaystyle \lim_(x\to\infty)(√(x)+5x^2)/(3x-1) = \lim_(x\to\infty)x \cdot \lim_(x\to\infty)\frac{\frac1{\sqrt x}+5x}{3x-1} = \lim_(x\to\infty)x \cdot \lim_(x\to\infty)\frac{\frac1{x^(3/2)}+5}{3-\frac1x} = \frac53\lim_(x\to\infty)x = \infty`

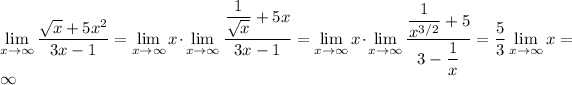
G) For a regular polynomial (unless you left out a denominator), the leading term determines the end behavior. In other words, for large x, x ⁴ is much larger than x ², so effectively

`\displaystyle \lim_(x\to\infty)(x^4-2x) = \lim_(x\to\infty)x^4 = \boxed{\infty}`