The transformed equation, with
 in terms of
in terms of
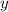 , is
, is
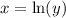 . therefore, option C is correct
. therefore, option C is correct
The image shows multiple choice options for a transformed version of the equation
 . To find the form of
. To find the form of
 in terms of
in terms of
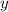 , we need to apply logarithmic operations because the equation involves the exponential function
, we need to apply logarithmic operations because the equation involves the exponential function
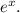
Here's the step-by-step process to solve for
 :
:
1. Start with the given equation:
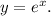
2. To solve for \( x \), take the natural logarithm (ln) of both sides of the equation to get the exponent on its own. This works because
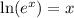 , which is the inverse operation of the exponential function.
, which is the inverse operation of the exponential function.
3. You'll end up with
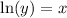 .
.
So the transformed equation, with
 in terms of
in terms of
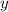 , is
, is
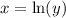 . This corresponds to one of the choices given in the image. No further calculation is necessary, as this is a direct application of logarithmic properties.
. This corresponds to one of the choices given in the image. No further calculation is necessary, as this is a direct application of logarithmic properties.