Question

What is the radius of the cone

Answer 1

5 is the answer !!!!!!

Answer 2

Explanation:

You can use calculus to derive the equation for the volume of a cone.

if we take an circle at the tip of the cone the radius is 0 but what we want to do is integrate along the x axis from 0 up to the height of the cone H.

So, the equation becomes

`\int\limits^H_0 {\pi r^(2) } \, dx`

r is related to x by the formula for a line; r = m*x+b

m is the rise over the run which is given by the maximum height H divided by the maximum radius R. So m = H/R and the intercept b = 0

now we have a formula for r in terms of x and with a little variable manipulation we can get a formula for x in terms of r

r = (R/H)*x

If we replace r by this formula in our integral we get:

`\int\limits^H_0 {\pi ((R/H)*x)^(2) } \, dx`

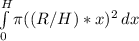
since
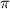`\pi`, R, and H are constants we can move them outside the integral:

`\pi (R^(2) /H^(2) )*\int\limits^H_0 {x^(2) } \, dx`

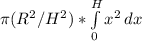
the integral is easy. It is
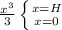`(x^(3))/(3)\left \{{{x=H}\atop{x=0}} \right.` which is equal to
`H^(3) /3`

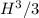
substituting back into the original formula we get the equation for the volume of a cone.
V =
`(\pi R^(2)H)/3`

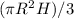
Use this formula with the values given in the question to solve for R.

183.17 =
`\pi`
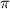
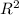`R^(2)`*7/3

rearranging we get

`√(183.17*3/(7\pi ) )` = R

R ≅ 5