Question

HELP PLEASE! IM STUCK--

Answer 1

9514 1404 393

Answer:

A (first choice), F (last choice)

Explanation:

Formulas for arithmetic sequences are generally written in one of two forms. The form you're given here is called an "explicit" formula. For some value of n, you can find the n-th term by evaluating the formula.

The form used in the first three answer choices is called a "recursive" formula. The value of the n-th term depends not on 'n', but on the previous term.

These two forms can be converted to each other like this:

explicit formula ⇔ recursive formula

`A(n)=A_1+d(n-1)\quad\Leftrightarrow\quad\begin{cases}a_1=A_1\\a_n=a_(n-1)+d\end{cases}`

The values of the first term (A₁), the common difference (d), and the term index number (n) are the same in both forms. Once you see this relationship, you should be able to find ...

• the first term
• the common difference
• the other formula for the same sequence

__

Here, the given function tells you ...

• A₁ = 5
• d = +4

This means the formulas that describe the same sequence are ...

`\square\ \begin{cases}a_1=5\\a_n=a_(n-1)+4\end{cases}\\\\\square\ A(n)=5+4(n-1)`

_____

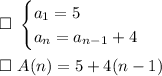
Additional comment

The commutative property of multiplication tells you that (n-1)(4) = 4(n-1). The order of the operands makes no difference. The given function has the first of these forms, the offered answer choices have the second of these forms.