Answer:
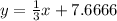
Explanation:
First we must convert
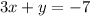 into slope-intercept form!
into slope-intercept form!
To do this we simply just need to subtract -3x from the 3x on the left and move it to the right side. This would result in:
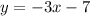
Now that we have our slope-intercept form for the equation remember that to find the equation that is perpendicular to the given equation, you need to use the opposite reciprocal of the slope. This would be
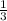 as that is the reciprocal and opposite of
as that is the reciprocal and opposite of
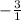
Now in order to find the "b" variable of the equation that goes through the ordered pair (1, 8) we need to plug it in to the given equation!
That equation would be:
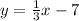
Given that x = 1 and y = 8 we can plug those in like so:
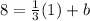
(make sure to set the -7 to b as that's what we're solving for)
1 / 3 is 0.3333 (infinitely repeating)
Next we need to subtract 0.3333 from 8, which would be 7.6666 (infinitely repeating) Remember that the variable needs to be "alone"!
Now we have our "b" for the equation! Hence the equation would be:
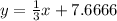
(you can also use
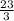 for the b as that is the "exact form" of 1 / 3 but they both work)
for the b as that is the "exact form" of 1 / 3 but they both work)
Hope this helps! Feel free to ask questions!