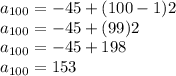Question

CAN ANYBODY HELP ME What is the 100th term in the sequence beginning with -45, -43, -41, -39, ...?

Group of answer choices


153


150


155


200


55

Answer 1

153

Explanation:

Since the given sequence is arithmetic because it has common difference.

-43-(-45) ,= -43+45 = 2

-41+43 = 2

-39+41 = 2

Therefore, the common difference is 2.

General Term

`\displaystyle \large{a_n = a_1 + (n - 1)d}`

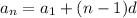
Since we want to find the 100th term, substitute n = 100.

We know common difference which is 2 and defined as 'd'; substitute d = 2

a1 means first term so:-

`\displaystyle \large{a_(100)= - 45 + (100 - 1)2} \\ \displaystyle \large{a_(100)= - 45 + (99)2} \\ \displaystyle \large{a_(100)= - 45 + 198} \\ \displaystyle \large{a_(100)= 153}`