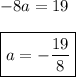Question

how to use Lcd in this problem? [a-2. -_1_ =_3_]find Lcd [ a+3 1 a-2]. (a+3)(a+2). multiply all neumerator to (LCD) a-2 - 1= 3 ___ _ a/+3. a+/2 (a-6 )(a+6) - 1 (a+2)(a+3)(a+2/)/*) negative a +positive2: distribuet: (a(a+3)++2. = (a+3)​

Answer 1

It's not entirely clear to me what you're trying to solve, but it looks like the initial equation is

`(a-2)/(a+3) -1 = \frac3{a+2}`

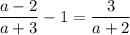
First convert each term into a fraction with the same (i.e. the least common) denominator. The first term needs to be multiplied by a + 2; the second term by (a + 3) (a + 2); and the third term by a + 3 :

`(a-2)/(a+3)\cdot(a+2)/(a+2) -1\cdot((a+3)(a+2))/((a+3)(a+2)) = \frac3{a+2}\cdot(a+3)/(a+3) \\\\ ((a-2)(a+2))/((a+3)(a+2)) - ((a+3)(a+2))/((a+3)(a+2)) = (3(a+3))/((a+3)(a+2))`

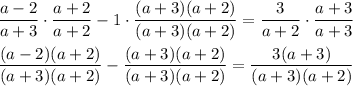
Now that everything has the same denominator, we can combine the fractions into one. Move every term to one side and join the numerators:

`((a-2)(a+2)-(a+3)(a+2)-3(a+3))/((a+3)(a+2)) = 0`

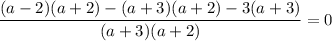
Simplify the numerator:

`((a^2-4)-(a^2+5a+6)-(3a+9))/((a+3)(a+2)) = 0 \\\\ (-8a-19)/((a+3)(a+2)) = 0`

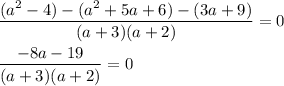
If neither a = -3 nor a = -2, we can ignore the denominator:

`-8a-19 = 0`

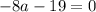
Solve for a :

`-8a = 19 \\\\ \boxed{a = -\frac{19}8}`