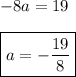It's not entirely clear to me what you're trying to solve, but it looks like the initial equation is
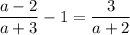
First convert each term into a fraction with the same (i.e. the least common) denominator. The first term needs to be multiplied by a + 2; the second term by (a + 3) (a + 2); and the third term by a + 3 :
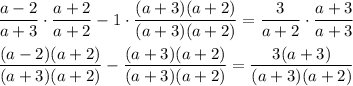
Now that everything has the same denominator, we can combine the fractions into one. Move every term to one side and join the numerators:
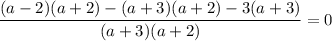
Simplify the numerator:
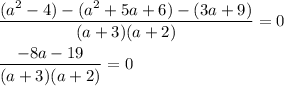
If neither a = -3 nor a = -2, we can ignore the denominator:
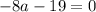
Solve for a :