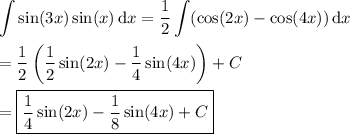Question

Integration of sin3xsinx

Answer 1

Recall that

cos(x + y) = cos(x) cos(y) - sin(x) sin(y)

cos(x - y) = cos(x) cos(y) + sin(x) sin(y)

If you subtract the first equation from the second one, you end up with

cos(x - y) - cos(x + y) = 2 sin(x) sin(y)

so that

sin(3x) sin(x) = 1/2 (cos(3x - x) - cos(3x + x)) = 1/2 (cos(2x) - cos(4x))

Then in the integral,

`\displaystyle \int \sin(3x)\sin(x)\,\mathrm dx = \frac12 \int(\cos(2x)-\cos(4x))\,\mathrm dx \\\\ = \frac12 \left(\frac12 \sin(2x) - \frac14 \sin(4x)\right) + C \\\\ = \boxed{\frac14 \sin(2x) - \frac18 \sin(4x) + C}`