Answer:
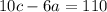
Explanation:
We are given the equation:
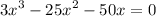
Where a, b, and c are solutions to the equation and where a < b < c, we want to determine the value of 10c - 6a.
To find the solutions of the equation, we can factor:
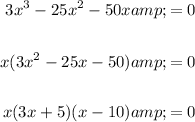
From the Zero Product Property:
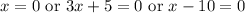
Solve for each case:
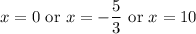
We can see that -5/3 < 0 < 10. Thus, a = -5/3, b = 0, and c = 10.
Therefore:
