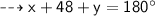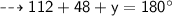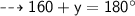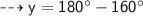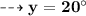There are two ways , so the first part reference to method 1 and and second part reference to method 2.

PART 1 :-

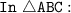

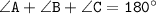
{sum of triangle}

here we can find value of angle C.

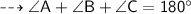

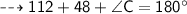

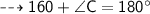

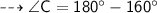

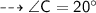

angle c is congruent to angle f
.°. y = 20°

PART 2:-

angle a = angle d
.°. value of x = 112°

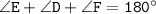

ve can find value of y :-