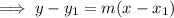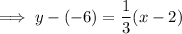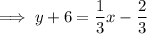Question

7

Write the equation of a line that is perpendicular to y = -3 + 6 and that passes through the point
(2,-6).

Answer 1

Perpendicular lines are lines that are at right angles to each other.

For perpendicular lines, the product of their slopes is -1.

`\implies m_2=(-1)/(m_1)`

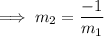
(where
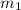`m_1` and
`m_2` are the slopes of perpendicular lines)

The slope of the given equation is -3. Therefore, to find the slope of the line that is perpendicular:

`m_2=(-1)/(-3)=\frac13`

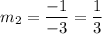
Now we have the slope, we can use the point-slope form of a linear equation with
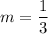`m=\frac13` and
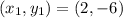`(x_1,y_1)=(2,-6)` to find the equation of the perpendicular line:

`\implies y-y_1=m(x-x_1)`

`\implies y-(-6)=\frac13(x-2)`

`\implies y+6=\frac13x-\frac23`

`\implies y=\frac13x-\frac{20}3`