Answer:
x = 2, x = 8
Explanation:
reminder that f'(x) =
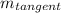
Differentiate f(x) term by term using the power rule
 (a
(a
 ) = na
) = na
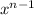
f(x) =
 x³ - 5x² + 2x + 10
x³ - 5x² + 2x + 10
f'(x) = x² - 10x + 2
Equating f'(x) to - 14
x² - 10x + 2 = - 14 ( add 14 to both sides )
x² - 10x + 16 = 0 ← in standard form
(x - 2)(x - 8) = 0 ← in factored form
Equate each factor to zero and solve for x
x - 2 = 0 ⇒ x = 2
x - 8 = 0 ⇒ x = 8