|| ▼ Answer ▼ ||
The orbital period is 31.62 years when the average distance from the sun is 10AU
|| ✪ Step-by-step explanation✪ ||
Given:
The average distance of the planet from the sun is r = 10 AU
To find the orbital period.
According to Kepler's third law,
 ∞
∞
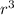
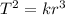
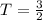
Here, the constant k is taken to be 1.
Substituting the values, the orbital speed will be


Final Answer: The orbital period is 31.62 years when the average distance from the sun is 10AU
Hope this helps!
If you have any queries please ask.