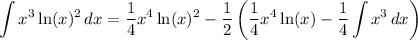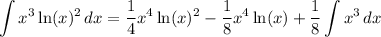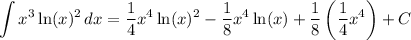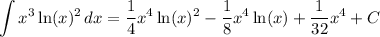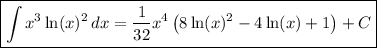Question

Integrala x la a treia ori ln la a doua dx va rog

Answer 1

I don't speak Romanian, but the closest translation for this suggests you're trying to compute

`\displaystyle \int x^3 \ln(x)^2 \, dx`

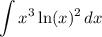
Integrate by parts:

`\displaystyle \int x^3 \ln(x)^2 \, dx = uv - \int v \, du`

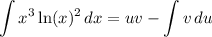
where

u = ln(x)² ⇒ du = 2 ln(x)/x dx

dv = x³ dx ⇒ v = 1/4 x⁴

`\implies \displaystyle \int x^3 \ln(x)^2 \, dx = \frac14 x^4 \ln(x)^2 - \frac12 \int x^3 \ln(x) \, dx`

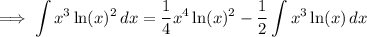
Integrate by parts again:

`\displaystyle \int x^3 \ln(x) \, dx = u'v' - \int v' du'`

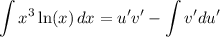
where

u' = ln(x) ⇒ du' = dx/x

dv' = x³ dx ⇒ v' = 1/4 x⁴

`\implies \displaystyle \int x^3 \ln(x) \, dx = \frac14 x^4 \ln(x) - \frac14 \int x^3 \, dx`

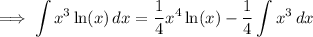
So, we have

`\displaystyle \int x^3 \ln(x)^2 \, dx = \frac14 x^4 \ln(x)^2 - \frac12 \left(\frac14 x^4 \ln(x) - \frac14 \int x^3 \, dx \right)`

`\displaystyle \int x^3 \ln(x)^2 \, dx = \frac14 x^4 \ln(x)^2 - \frac18 x^4 \ln(x) + \frac18 \int x^3 \, dx`

`\displaystyle \int x^3 \ln(x)^2 \, dx = \frac14 x^4 \ln(x)^2 - \frac18 x^4 \ln(x) + \frac18 \left(\frac14 x^4\right) + C`

`\displaystyle \int x^3 \ln(x)^2 \, dx = \frac14 x^4 \ln(x)^2 - \frac18 x^4 \ln(x) + \frac1{32} x^4 + C`

`\boxed{\displaystyle \int x^3 \ln(x)^2 \, dx = \frac1{32} x^4 \left(8\ln(x)^2 - 4\ln(x) + 1\right) + C}`