Answer:
678 ft (nearest foot)
Explanation:
The distance from the center of a circle its edge is its radius.
Given that the distance from the center of a circular tent to the tent’s edge is 50 ft then:
⇒ radius (r) = 50
The edge of a circle is its circumference
Circumference of a circle =
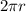 (where r is the radius)
(where r is the radius)
Therefore, the circumference of the tent is:
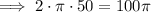 ft
ft
If Kelly walked around the edge of the tent twice, then walked straight to the center:
⇒ total distance walked = 2 × circumference + radius
= 2 ×
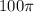 + 50
+ 50
= 678.3185307...
= 678 ft (nearest foot)