Question

Maximize P=6x+11y using simplex where

4x+y is less than/equal to 8
x+4y is less than/equal to 12
and x is greater than/equal to 0 , y is greater than/equal to 0

Answer 1

9514 1404 393

Answer:

(x, y, P) = (4/3, 8/3, 112/3)

Explanation:

In standard form, the constraints are all "less than or equal to", the variables are all non-negative, and the objective is maximization. This problem is presented in standard form.

4x +y ≤ 8

x +4y ≤ 12

x ≥ 0; y ≥ 0

maximize P = 6x +11y

__

Now we add the slack variables to make the constraints be "equal to". These have a coefficient of +1, and they, too, are non-negative. Here, we'll use s and t as the slack variables.

4x +y +s = 8

x +4y +t = 12

These equations, together with the objective function, are combined in a matrix-like "tableau" in which each row is the set of coefficients in one of the equations. Here, the columns represent x, y, s, t, P and the constants. The equation for the objective function is negated so we're trying to minimize that, as well.

`\begin{array}ccccc4&1&1&0&0&8\\1&4&0&1&0&12\\-6&-11&0&0&1&0\end{array}`

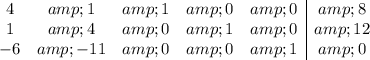
Find the column with the most negative value on the bottom row. (Column 2) Divide the rightmost column by this column and find the smallest quotient. Here, the quotients are 8/1 = 8, and 12/4 = 3. The smallest is 3. This identifies the 4 in column 2, row 2 as the "pivot."

Now, row operations are performed to make the pivot be 1 and other values in the pivot column be zero. This gives a new tableau. For example, the new values in row 1 are ...

4 -1/4, 1 -4/4, 1 -0/4, 0 -1/4, 0 -0/4, 8 -12/4

The new tableau is ...

`\begin{array}c15/4&0&1&-1/4&0&5\\1/4&1&0&1/4&0&3\\-13/4&0&0&11/4&1&33\end{array}`

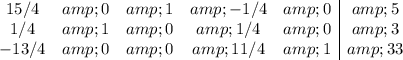
Now, the most negative number on the bottom row is in column 1, and the smallest quotient of column 6 and column 1 is in row 1. This makes 15/4 the "pivot". After the required row operations, the next tableau is ...

`\begin{array}c1&0&4/15&-1/15&0&4/3\\0&1&-1/15&4/15&0&8/3\\0&0&13/15&38/15&1&112/3\end{array}`

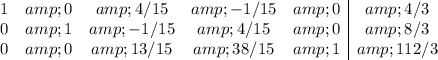
All values in the last row are non-negative, so we are finished. The rightmost column tells us the values of x, y, P that are the solution to the problem

(x, y, P) = (4/3, 8/3, 112/3)

__

The graphical solution confirms the Simplex solution.