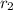 Answer:
Answer:
D) 96%
Explanation:
let the circumference of circle be C = 2π
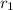 and
and
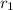 =
=
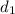 /2
/2
Initial radius (radius before increment) =
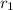
initial diameter (diameter before increment) =
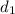
Increasing the circumference of a circle other factors are constant except the radius which can be used to find the diameter hence increasing the circumference of a circle is equivalent to increasing the diameter
area of the circle before increment
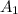 = π
= π
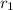 ²
²
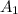 = π × (
= π × (
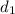 /2)²
/2)²
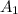 = π
= π
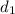 ²/4
²/4
Increment of circumference results to increment of only the diameter
diameter after increment by 40%,
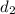 = 1.4
= 1.4
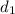
1.4 represents increment by 40%
radius after increment
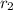 =
=
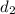 /2 = 1.4
/2 = 1.4
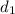 /2 = 0.7
/2 = 0.7
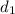
area after increment,
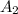 = π
= π
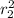
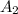 = π(0.7
= π(0.7
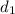 )²
)²
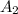 = π × 0.49
= π × 0.49
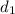 ²
²
Change in area =
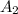 -
-
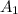
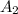 -
-
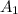 = π × 0.49
= π × 0.49
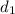 ² - π
² - π
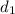 ²/4
²/4
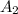 -
-
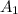 = π
= π
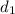 ²(0.49 - ¼)
²(0.49 - ¼)
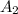 -
-
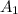 = π
= π
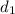 ²(0.49 - 0.25)
²(0.49 - 0.25)
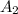 -
-
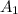 = 0.24 π
= 0.24 π
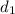 ²
²
Percentage increment = (
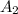 -
-
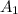 /
/
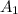 ) × 100
) × 100
= ((0.24 π
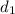 ²)/(π
²)/(π
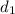 ²/4)) × 100
²/4)) × 100
= (0.24 × 4 ) × 100
= 0.96 × 100
= 96 %
Hope it was useful