Answer:
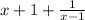
Explanation:
Reformatting the input :
Changes made to your input should not affect the solution:
(1): "x2" was replaced by "x^2". 1 more similar replacement(s).
STEP
1
:
Equation at the end of step 1
STEP
2
:
x3 - 2x2 + 2x - 1
Simplify —————————————————
x - 1
Checking for a perfect cube :
2.1 x3 - 2x2 + 2x - 1 is not a perfect cube
Trying to factor by pulling out :
2.2 Factoring: x3 - 2x2 + 2x - 1
Thoughtfully split the expression at hand into groups, each group having two terms :
Group 1: 2x - 1
Group 2: -2x2 + x3
Pull out from each group separately :
Group 1: (2x - 1) • (1)
Group 2: (x - 2) • (x2)
Bad news !! Factoring by pulling out fails :
The groups have no common factor and can not be added up to form a multiplication.
Polynomial Roots Calculator :
2.3 Find roots (zeroes) of : F(x) = x3 - 2x2 + 2x - 1
Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0
Rational Roots Test is one of the above mentioned tools. It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers
The Rational Root Theorem states that if a polynomial zeroes for a rational number P/Q then P is a factor of the Trailing Constant and Q is a factor of the Leading Coefficient
In this case, the Leading Coefficient is 1 and the Trailing Constant is -1.
The factor(s) are:
of the Leading Coefficient : 1
of the Trailing Constant : 1
Let us test ....
P Q P/Q F(P/Q) Divisor
-1 1 -1.00 -6.00
1 1 1.00 0.00 x - 1
The Factor Theorem states that if P/Q is root of a polynomial then this polynomial can be divided by q*x-p Note that q and p originate from P/Q reduced to its lowest terms
In our case this means that
x3 - 2x2 + 2x - 1
can be divided with x - 1
Polynomial Long Division :
2.4 Polynomial Long Division
Dividing : x3 - 2x2 + 2x - 1
("Dividend")
By : x - 1 ("Divisor")
dividend x3 - 2x2 + 2x - 1
- divisor * x2 x3 - x2
remainder - x2 + 2x - 1
- divisor * -x1 - x2 + x
remainder x - 1
- divisor * x0 x - 1
remainder 0
Quotient : x2-x+1 Remainder: 0
Trying to factor by splitting the middle term
2.5 Factoring x2-x+1
The first term is, x2 its coefficient is 1 .
The middle term is, -x its coefficient is -1 .
The last term, "the constant", is +1
Step-1 : Multiply the coefficient of the first term by the constant 1 • 1 = 1
Step-2 : Find two factors of 1 whose sum equals the coefficient of the middle term, which is -1 .
-1 + -1 = -2
1 + 1 = 2
Observation : No two such factors can be found !!
Conclusion : Trinomial can not be factored
Canceling Out :
2.6 Cancel out (x-1) which appears on both sides of the fraction line.
Final result :
x2 - x + 1