Answer:
see explanation
Explanation:
Using identities
sec²x = tan²x + 1
cosec²x = cot²x + 1
cos²x =
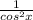
(1)
sin²θ +
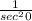
= sin²θ + cos²θ = 1
(2)
9sec²θ - 9tan²θ
= 9sec²θ - 9(sec²θ - 1)
= 9sec²θ - 9sec²θ + 9
= 9
(3)
- 8cot²A + 8cosec²A
= - 8cot²A + 8(cot²A + 1)
= - 8cot²A + 8cot²A + 8
= 8
(4)
- 10cosec²β + 10cot²β
= - 10(cot²β + 1) + 10cot²β
= - 10cot²β - 10 + 10cot²β
= - 10