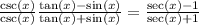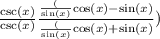Question

1) Given A = {1, 2, 3, 4, 5 }; B = {2,4,6,83 2,4,6,8} Find A∩B, A-B

2) Is it true to say that sin ( A+B) = -sinA + sinB

3) prove that ( tan theta - sin theta ) / ( tan theta + sin theta ) = ( sec theta - 1 ) / ( sec theta + 1 ) ​

Answer 1

A∩B = 2,4

A-B = 1,3,5

sin (A+B) = sin(A)cos(B)+cos(A)sin(B)

Explanation:

A intersects U means the numbers that are coming to both A and U

set a minus set b of the numbers that are not common to B

multiply the numerator and the denominator by csc(x)

NOTE: I substituted x for theta as I don't have theta on my phone

`( \csc(x) )/( \csc(x)) ( \tan(x) - \sin(x) )/( \tan(x) + \sin(x) ) = ( \sec(x) - 1)/( \sec(x) + 1)`

`\frac {\csc(x)}{\csc(x)} \frac {\frac ({\sin(x)}{\cos(x)}-\sin(x)} {\frac ({\sin(x)}{\cos(x)} + \sin(x)})`