This is one pathway to prove the identity.
Part 1
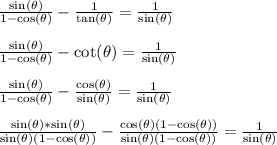
Part 2

Part 3
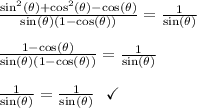
As the steps above show, the goal is to get both sides be the same identical expression. You should only work with one side to transform it into the other. In this case, the left side transforms while the right side stays fixed the entire time. The general rule is that you should convert the more complicated expression into a simpler form.
We use other previously established or proven trig identities to work through the steps. For example, I used the pythagorean identity
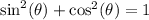 in the second to last step. I broke the steps into three parts to hopefully make it more manageable.
in the second to last step. I broke the steps into three parts to hopefully make it more manageable.