Question

Write the equation of the line that passes through the points (-3, -3) and (8,7).

Put your answer in fully reduced point-slope form, unless it is a vertical or horizontal
line.

Answer 1

y + 3 = 10/11(x + 3)

Explanation:

Given the points (-3, -3) and (8, 7), we can use these coordinates to solve for the slope of the line using the formula:

`m = (y2 - y1)/(x2 - x1)`

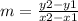
Let (x1, y1) = (-3, -3)

(x2, y2) = (8, 7)

Substitute these values into the slope formula:

`m = (y2 - y1)/(x2 - x1) = (7 - (-3))/(8 - (-3)) = (10)/(11)`

Thus, slope (m) = 10/11.

Next, using the slope (m) = 10/11, and one of the given points (-3, -3), we'll substitute these values into the point-slope form:

y - y1 = m(x - x1)

Let (x1, y1) = (-3, -3)

m = 10/11

y - y1 = m(x - x1)

y - (-3) = 10/11[x - (-3)]

Simplify:

y + 3 = 10/11(x + 3) this is the point-slope form.