Question

Given the system of equations, what is the solution?

2x + y = 7
2x - 3y = -1

Answer 1

`((5)/(2), 2)`

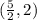
Explanation:

Hi there!

We are given this system of equations:

2x + y = 7

2x - 3y = -1

And we want to find the solution

There are multiply ways to solve systems of equations, but let's solve this one by elimination, where we will add the two equations together to clear one of them, solve for the un-cleared variable, and then use the value of the un-cleared variable to solve for the cleared one

Before clearing a variable, we need to make sure that the signs on the variables are opposites; for example, -3 and 3, which will add together to get 0

We can multiply the equations beforehand if needed in order to manipulate the numbers.

For example, we can multiply the second equation by -1 in order to switch the signs of each number in that equation:

-1(2x-3y=-1)

-2x+3y=1

Now the signs in front of x are 2 and -2, so we can add the equations together to clear them:

2x + y = 7

-2x + 3y = 1

Add the equations together

4y = 8

Divide both sides by 4

y=2

Now let's use 2 as y to solve for x

In the first equation, substitute 2 for y:

2x + 2 = 7

Subtract 2 from both sides

2x = 5

Divide both sides by 2

`x=(5)/(2)`

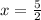
As a point, the answer is
`((5)/(2), 2)`

Hope this helps!