Question

If a²+b²=8ab, determine (a+b) in terms of a and b​

Answer 1

[The question's not wholly right! Since, (a+b) has a and b in it, it already is in terms of a and b. Here, we'll be representing (a+b) in terms of ab]

Answer:

`\mathsf{√(10ab) }`

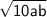
Explanation:

We have the rules of indices, one of which is:

`\boxed{\large{\mathfrak{(a+b)^2=a^2+b^2+2ab}}}`

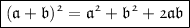
Indices are the powers, the numbers written as superscript in front of a variable or the numbers that come along with "^". It shows how many times a number is to be multiplied by itself.

In the question, we're provided with one equation, i. e.,

• a² + b² = 8ab . . . . . . . . (¡)

And, were asked to find out the value of (a+b) in terms of ab.

The above rule has variables that fit in the question efficiently!

So, instead of solving for (a+b), we'll be solving for (a+b)², then go for (a + b):

=> (a + b)² = (a² + b²) + 2ab

from eqn. (¡):

=> (a + b)² = 8ab + 2ab

=> (a + b)² = 10ab

taking under root on both the sides:

=> (a + b) =
`\mathsf{√(10ab) }`

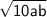
That's the answer,
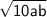`\mathsf{√(10ab) }`!

`\overline{\mathfrak{Hope \:this \:makes\: sense!}}`