Question

A car covers the distance between two cities in 6 hours. A van covers the same distance in 5.5 hours by travelling 4 km/h faster than the car. What is the distance between the two cities? Find the speed of the car and the van.​

Answer 1

Explanation:

`\large\underline{\sf{Solution-}}`

Given that,

A car covers the distance between two cities in 6 hours.

A van covers the same distance in 5.5 hours.

The speed of the van is 4 km per hour faster than the speed of car.

Let assume that

Speed of the car be x km per hour

So,

Speed of van is x + 4 km per hour.

Let further assume that

Distance between two cities be y km.

We know, Distance covered = Speed × Time.

➢ Now, Distance (y) covered by car at the speed of x km per hour in 6 hours is

`\rm :\longmapsto\:\boxed{\tt{ y = 6x}} - - - - (1)`

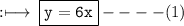
➢ Also, Distance (y) covered by van at the speed of x + 4 km per hour in 5.5 hours is

`\rm :\longmapsto\:\boxed{\tt{ y = 5.5(x + 4)}} - - - - (2)`

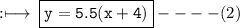
So, from equation (1) and (2), we have

`\rm :\longmapsto\:6x = 5.5(x + 4)`

`\rm :\longmapsto\:6x = 5.5x + 22`

`\rm :\longmapsto\:6x - 5.5x = 22`

`\rm :\longmapsto\:0.5x = 22`

`\rm :\longmapsto\:(5)/(10) * x = 22`

`\rm :\longmapsto\:(1)/(2) * x = 22`

`\bf\implies \:x = 44`

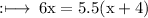
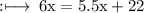
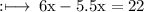
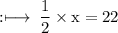
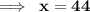
On substituting the value of x, in equation (1), we have

`\rm :\longmapsto\:y = 6 * 44`

`\bf\implies \:y = 264`

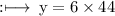
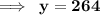
So,

`\begin{gathered}\begin{gathered}\bf\: \rm :\longmapsto\:\begin{cases} &\sf{Distance \: between \: cities = 264 \: km} \\ \\ &\sf{Speed \: of \: car \: = \: 44 \: km \: per \: hour}\\ \\ &\sf{Speed \: of \: van \: = \: 48 \: km \: per \: hour} \end{cases}\end{gathered}\end{gathered}`