Question

3. In a figure a small square is cutting out from the largesquare. The area of the remaining part is 91 cm². The sum of Sides equal to 52cm.

(a). If the side of large square is x and the side of smallest square is y then find the area of the remaining part?
(b). Find the sides of the smallest square?
(c). Find the areas of the two squares?​

Answer 1

Explanation:

`\large\underline{\sf{Solution-}}`

Given that,

1. ABCD is a square of side x cm

1. EFGH is a square of side y cm

Further given that,

1. Sum of all sides = 52 cm

It means

• Perimeter of square ABCD + Perimeter of square EFGH is 52 cm

We know,

`\purple{\rm :\longmapsto\:\boxed{\tt{ Perimeter_([square]) \: = \: 4 * side \: }}}`

So, using this, we have

`\rm :\longmapsto\:4x + 4y = 52`

`\rm :\longmapsto\:4(x + y) = 52`

`\rm\implies \:\boxed{\tt{ x + y = 13}} - - - - (1)`

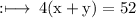
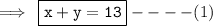
Now, Further given that,

If square EFGH is cutting out from square ABCD, the area of remaining part is 91 square cm.

It means

`\rm :\longmapsto\:Area_([ABCD]) - Area_([EFGH]) = 91`

We know,

`\purple{\rm :\longmapsto\:\boxed{\tt{ Area_([square]) = 4 * side}}}`

So, using this, we get

`\rm :\longmapsto\: {x}^(2) - {y}^(2) = 91`

can be further rewritten as using algebraic Identity,

`\rm :\longmapsto\:(x + y)(x - y) = 91`

`\rm :\longmapsto\:13(x - y) = 91`

`\red{ \bigg\{  \sf \: \because \: using \: equation \: (1) \bigg\}}`

`\rm\implies \:\boxed{\tt{ x - y = 7}} - - - - (2)`

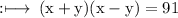
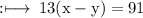
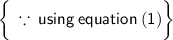
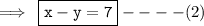
On adding equation (1) and (2), we get

`\rm :\longmapsto\:2x = 13 + 7`

`\rm :\longmapsto\:2x = 20`

`\rm\implies \:\boxed{ \: \bf \: \: x \: = \: 10 \:cm \: \: }`

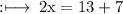
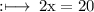
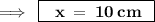
On substituting the value of x in equation (1), we have

`\rm :\longmapsto\:10 + y = 13`

`\rm :\longmapsto\:y = 13 - 10`

`\rm\implies \:\boxed{ \: \bf \: \: y \: = \: 3 \:cm \: \: }`

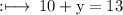
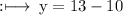
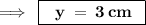
So,

`\rm\implies \:\boxed{Side_([square \: EFGH]) = y \: = 3 \: cm}`

and

`\rm\implies \:\boxed{Side_([square \: ABCD]) = x \: = 10 \: cm}`

Also,

`\rm :\longmapsto\:\boxed{Area_([square \: ABCD]) = {10}^(2) = 100 \: {cm}^(2) }`

`\rm :\longmapsto\:\boxed{Area_([squareEFGH] )\: = {3}^(2) = 9 \: {cm}^(2) }`

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

`\begin{gathered}\begin{gathered}\boxed{\begin {array}{cc}\\ \dag\quad \Large\underline{\bf Formulas\:of\:Areas:-}\\ \\ \star\sf Square=(side)^2\\ \\ \star\sf Rectangle=Length* Breadth \\\\ \star\sf Triangle=(1)/(2)* Breadth* Height \\\\ \star \sf Scalene\triangle=\sqrt {s (s-a)(s-b)(s-c)}\\ \\ \star \sf Rhombus =\frac {1}{2}* d_1* d_2 \\\\ \star\sf Rhombus =\:\frac {1}{2}d\sqrt {4a^2-d^2}\\ \\ \star\sf Parallelogram =Breadth* Height\\\\ \star\sf Trapezium =\frac {1}{2}(a+b)* Height \\ \\ \star\sf Equilateral\:Triangle=\frac {√(3)}{4}(side)^2\end {array}}\end{gathered}\end{gathered}`