Question

Help would be appreciated!
Please explain how you got the answer c:

Answer 1

Let's see

`\\ \rm\Rrightarrow {\displaystyle{\sum^2_(k=1)}}(2k-11)`

• k=1,2,3,4,5

`\\ \rm\Rrightarrow 2(1)-11+2(2)-11+2(3)-11+2(4)-11+2(5)-11`

`\\ \rm\Rrightarrow 2-11+4-11+6-11+8-11+10-11`

`\\ \rm\Rrightarrow 30-55`

`\\ \rm\Rrightarrow -25`

Answer 2

-25

Explanation:

Reading the expression:

We're given the sigma notation of a series.

`\mathsf{ \sum _(k = 1) ^(5)(2k - 11) }`

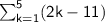
The variable k is the "index of notation"

The expression can be read as the sum of (2k- 11) as k goes from 1 to 5.

"To generate the terms of a series given in sigma notation, successively replace the index of summation with consecutive integers from the first value to the last value of the index" ~internet

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Generating the terms of the series:

To generate the terms of the series given on sigma notation above, replace k by 1, 2, 3, 4, and 5 and add the terms, to get the answer to the given notation.

`\mathsf{ \sum _(k = 1) ^(5)(2k - 11) } \\ = \mathsf{ \overline{2(1) - 11} + \overline{2(2) - 11} + \overline{2(3) - 11} } \\ \mathsf{ + \overline{2(4) - 11} + \overline{2(5) - 11}}`

`= \mathsf{\overline{2 - 11} +\overline{4 - 11} + \overline{6 - 11} } \\ \mathsf{\overline{8 - 11} + \overline{10- 11}}`

`= \mathsf{ - 9- 7 - 5 - 3 - 1}`

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

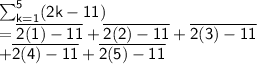
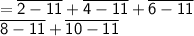
Final Answer:

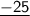
`\mathsf{ \underline{- 25}}`

______________________

`\mathfrak{ \overline{There \: You \: Are!}}`