Question

Can I get help on 1,2 and 5?

Answer 1

Question 1:
`x=4`

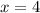
Question 2:
`x= \pm7`

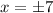
Question 5: The dimensions of one face of the container are 6 by 6 inches.

Explanation:

Hi there!

Question 1

`x^3=64`

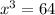
Rewrite 64 as a power of 3:

`x^3=4^3`

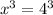
(We could find that 4³ = 64 through trial and error)

This above equation makes it true that x=4. If aⁿ = bⁿ, then a=b:

`x=4`

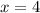
Question 2

`x^2=49`

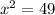
Rewrite 49 as a power of 2:

`x^2=7^2`

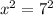
Again, we could have found this through trial and error, or by looking at our multiplication tables.

`x=7`

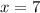
However, remember that positive and negative numbers will all square to be a positive number. So, therefore, x can be -7 OR 7 (since both, when squared, equal 49):

`x= \pm7`

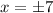
Question 5

Let x be equal to the length of one edge of the cube.

Volume of a cube formula:
`V=x^3`

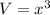
Plug in the given information, when V is the volume:

`216=x^3`

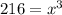
Rewrite 216 as a power of 3:

`6^3=x^3`

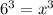
^ We could have found this through trial and error.

`x=6`

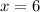
Therefore, the dimensions of one face of the container are 6 by 6 inches.

I hope this helps!