Question

Let f(x)=
`\footnotesize \rm \lim_(n \to \infty ) \left \lgroup \frac{ {n}^n(x + n) \bigg( x + (n)/( 2) \bigg) \dots \bigg(x + (n)/(n) \bigg)}{n!( {x}^(2) + {n}^(2)) \bigg( {x}^(2) + \frac{ {n}^2 }{4} \bigg) \dots \bigg( {x}^(2) + \frac{ {n}^(2) }{ {n}^(2) } \bigg) } \right \rgroup^{ (x)/(n) } \\` , for all x > 0. Then


`\rm(A) \: f \bigg( (1)/(2) \bigg ) \geq f(1)`


`\rm(B) \: f \bigg ( (1)/(3) \bigg) \leq f \bigg ( (2)/(3) \bigg)`


`\rm(C) \: f'(2) \leq0`


`\rm(D) \: (f'(3))/(f(3)) \geq (f'(2))/(f(2)) \\`​

Answer 1

Use the old exp-log trick and properties of the logarithm to rewrite the limit as

`\displaystyle \lim_(n\to\infty) \left((n^n \left(x+\frac n1\right) \left(x+\frac n2\right) \cdots \left(x+\frac nn\right))/(n! \left(x^2+\left(\frac n1\right)^2\right) \left(x^2+\left(\frac n2\right)^2\right) \cdots \left(x^2+\left(\frac nn\right)^2\right))\right)^(\frac xn)`

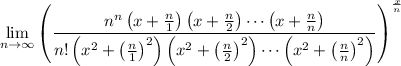
`\displaystyle = \exp\left[\lim_(n\to\infty) \frac xn \ln \left((n^n \left(x+\frac n1\right) \left(x+\frac n2\right) \cdots \left(x+\frac nn\right))/(n! \left(x^2+\left(\frac n1\right)^2\right) \left(x^2+\left(\frac n2\right)^2\right) \cdots \left(x^2+\left(\frac nn\right)^2\right))\right)\right]`

`\displaystyle = \exp\left[x \lim_(n\to\infty)\frac1n\ln\left((n^n)/(n!)\right) + \frac1n \sum_(k=1)^n \ln\left(x+\frac nk\right) - \frac1n \sum_(k=1)^n \ln\left(x^2+\left(\frac nk\right)^2\right)\right]`

`\displaystyle = \exp\left[x \lim_(n\to\infty)\frac1n\ln\left((n^n)/(n!)\right) + \frac1n \sum_(k=1)^n \ln\left(x+\frac1{k/n}\right) - \frac1n \sum_(k=1)^n \ln\left(x^2+\frac1{\left(k/n\right)^2}\right)\right]`

The first limit converges to 0, since n! asymptotically behaves like nⁿ, so ln(nⁿ/n!) → ln(1) = 0.

The two remaining sums converge to definite integrals:

`\displaystyle \lim_(n\to\infty) \frac1n \sum_(k=1)^n \ln\left(x + \frac1{\frac kn}\right) = \int_0^1 \ln\left(x + \frac1y\right) \, dy = \frac{(x+1) \ln(x+1)}x`

`\displaystyle \lim_(n\to\infty) \frac1n \sum_(k=1)^n \ln\left(x^2 + \left(\frac1{\frac kn}\right)^2\right) = \int_0^1 \ln\left(x^2 + \frac1{y^2}\right) \, dy = (2\tan^(-1)(\sqrt x))/(\sqrt x) + \ln(1+x)`

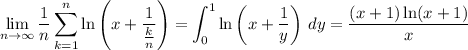
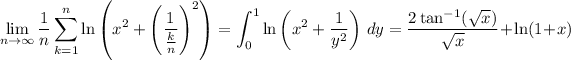
It follows that

`f(x) = \exp\left[x\left(0 + \frac{(x+1)\ln(x+1)}x - (2\tan^(-1)(\sqrt x))/(\sqrt x) - \ln(x+1)\right)\right]`

`f(x) = \exp\left[\ln(x+1) - 2\sqrt x \tan^(-1)(\sqrt x)\right]`

`f(x) = (x+1) e^{-2\sqrt x \tan^(-1)(\sqrt x)}`

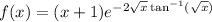
By computing f'(x) and f''(x), it's easy to show that f'(x) ≤ 0 and f''(x) ≥ 0 for all x > 0. So f(x) is decreasing and f'(x) is increasing, and

• (A) f(1/2) ≥ f(1) is true

• (B) f(1/3) ≤ f(2/3) is false

• (C) f'(2) ≤ 0 is true

• (D) f'(3)/f(3) ≥ f'(2)/f(2) ⟺ f'(3)/f'(2) ≥ f(3)/f(2) ⟺ (something larger than 1) ≥ (something smaller than 1) is true