Question

A line passes through the points (0, 9) and (9, 19). What is its equation in slope-intercept form?

Answer 1

y = 10/9x + 9

Explanation:

To write the equation in its slope-intercept form, y = mx + b, we need to find the slope (m) of the line and its y-intercept (b).

Given the points (0, 9) and (9, 19), we can solve for the slope of the line using the following formula:

`m = (y2 - y1)/(x2 - x1)`

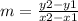
Let (x1, y1) = (0, 9)

and (x2, y2) = (9, 19)

Substitute these values on the formula:

`m = (y2 - y1)/(x2 - x1) = (19 - 9)/(9 - 0) = (10)/(9)`

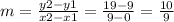
Therefore, the slope (m ) = 10/9.

Next, the y-intercept is the point on the graph where it crosses the y-axis, and has the coordinates, (0, b ). It is also the value of the y when x = 0.

One of the given points is the y-intercept of the line, given by (0, 9). The y-coordinate, 9, is the value of b.

Therefore, the linear equation in slope-intercept form is: y = 10/9x + 9