Question

A line passes through (-2,4), (-4, 8), and (n, -4). Find the value of n.

Answer 1

Answer: n = 2 ....... (2, -4)

Explanation:

To find n, one must write the equation for the points given, which are (-2, 4) and (-4, 8). Remember, the standard linear equation is y = mx + b, where m is the slope of the line.

To find the slope, refer back to (y2-y1)/(x2-x1), or in this case, (8-4)/(-4+2), which gives us -2

With our slope of -2, we can write the equation as y = -2x+b. Now, we need to find b (the y-intercept) by plugging in a point as (x,y)

Let's use (-4,8) point and plug it into our linear equation: y = -2x+b

to get 8=(-2)(-4) +b

8=8+b

0=b (which means our y-intercept is 0)

Now, our official linear equation is y=-2x

The problem gives us (n, -4) where -4 y, so we plug in -4 as y in the equation to get:

-4=-2x

-4/-2=x

2 = x

And there we go :) I hope this helps!

Answer 2

The value of n = 2.

Explanation:

Given the following points passing through a line, (-2, 4), (-4, 8), and (n , -4) wherein we must find the value of n:

It helps to determine the equation of the line, using the slope-intercept form: y = mx + b, where:

• m = slope (rate of change), which measures the steepness of the line.

• b = y-coordinate of the y-intercept; it is the point on the graph where it crosses the y-axis.

Slope:

In order to solve for the slope of the line, use the following slope formula:

`\displaystyle\mathsf{m =\:(y_2 - y_1)/(x_2 - x_1)}`

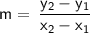
Let (x₁, y₁) = (-2, 4)

(x₂, y₂) = (-4, 8)

Substitute these values into the slope formula.

`\displaystyle\mathsf{m =\:(y_2 - y_1)/(x_2 - x_1)}`

`\displaystyle\mathsf{m =\:(8 - 4)/(-4 -(-2))\:=\:(4)/(-4+2)\:=\Frac{4}{-2}\:=\:-2}`

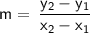
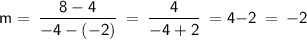
Hence, the slope of the line is: m = -2.

Y-intercept:

Next, we must solve for the y-intercept. Since it is the point where the graph crosses the y-axis, set x = 0 and solve for the value of y.

Use the slope, m = -2, and one of the given points, (-2, 4), and substitute these values into the slope-intercept form to solve for the value of the y-intercept, b:

y = mx + b

4 = -2(-2) + b

4 = 4 + b

Subtract 4 from both sides:

4 - 4 = 4 - 4 + b

0 = b

The y-intercept is: b = 0.

Linear Equation in Slope-intercept Form:

Therefore, the equation of the line in slope-intercept form is:

y = -2x + 0 or y = -2x.

Find the value of n in (n, -4)

In order to determine the value of n, substitute its corresponding y-coordinate, -4, and substitute into the equation in the previous step:

Set y = -4:

y = -2x

-4 = -2x

Divide both sides by -2 to solve for x:

`\displaystyle\mathsf{(-4)/(-2)\:=\:(-2x)/(-2)}`

x = 2

Therefore, the value of n = 2.