Answer:
Breadth/width = 1.936cm, length = 7.746cm
Explanation:
Perimeter of a rectangle would be
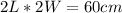 in this case. Breadth is width.
in this case. Breadth is width.
But we can rewrite this equation given that the width is 1/4 the length. This means 4 of the widths would equal one length.
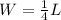
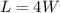
We can substitute L with the 4W
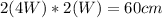
Now we can just solve for the width W.
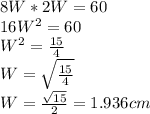
We now know the width is about 1.936cm
We can find the length given our formula before of
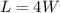
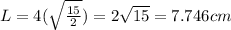
So the breadth/width is 1.936cm and the length is 7.746cm.