Answer:
a) 1/2
b) 250
Explanation:
The start of the question doesn't matter entirely, although is interesting to read. What we are trying to do is find the value for
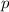 such that
such that
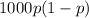 is maximized. Once we have that
is maximized. Once we have that
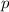 , we can easily find the answer to part b.
, we can easily find the answer to part b.
Finding the value that maximizes
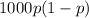 is the same as finding the value that maximizes
is the same as finding the value that maximizes
 , just on a smaller scale. So, we really want to maximize
, just on a smaller scale. So, we really want to maximize
 . To do this, we will do a trick called completing the square.
. To do this, we will do a trick called completing the square.
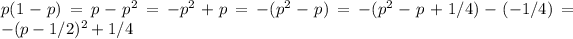 .
.
Because there is a negative sign in front of the big squared term, combined with the fact that a square is always positive, means we need to find the value of
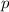 such that the inner part of the square term is equal to
such that the inner part of the square term is equal to
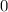 .
.
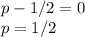 .
.
So, the answer to part a is
 .
.
We can then plug
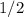 into the equation for p to find the answer to part b.
into the equation for p to find the answer to part b.
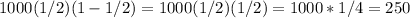 .
.
So, the answer to part b is
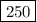 .
.
And we're done!