Answer:
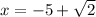 or
or
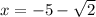
Explanation:
Step 1: Simplify both sides of the equation.
Step 2: Subtract 1 from both sides.
For this equation: a = 2, b = 20, c = 46
Step 3: Utilize quadratic formula with a = 2, b = 20, c = 46.
- x = (-20 ± √(20^2 - 4·2·46)/2(2)
- x = (-20 ± √(32)/4
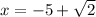 or
or
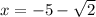
Therefore, the answer is
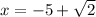 or
or
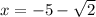 .
.