Question

What is the value of x, if twice x plus 3 cubed equals 40?

Answer 1

I will give two solutions, one where everything is cubed and one where just the 3 is cubed, because I don't know what you meant.

Just the 3 is cubed solution(Which I think is correct because it has a nicer answer):

Answer:

`13/2`

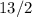
Explanation:

We have that
`2x+3^3=40`.

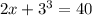We can subtract
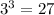`3^3=27` from both sides of the equation to get
`2x=13`.

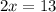We can then divide by
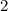`2` to get
`x=13/2`.

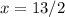So,
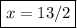`\boxed{x=13/2}` and we're done!

Everything is cubed solution:

Answer:

`\sqrt[3]{5}-3/2`

Explanation:

We have that
`(2x+3)^3=40`.

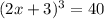We can take the cube root of both sides to get
`2x+3=\sqrt[3]{40}`.

Note that
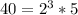`40=2^3*5`, so
`\sqrt[3]{40}=\sqrt[3]{2^3*5}=2\sqrt[3]{5}`.

So, we want to solve
`2x+3=2\sqrt[3]{5}`.

We can subtract
`3` from both sides to get
`2x=2\sqrt[3]{5}-3`.

We can then divide both sides by
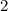`2` to get
`x=\sqrt[3]{5}-3/2`.

So,
`\boxed{x=\sqrt[3]{5}-3/2}` and we're done!