Assuming [x] means the closest integer to x
Answer:
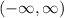
Explanation:
We can see that for any integer
 , there will always be a
, there will always be a
![[x]](https://img.qammunity.org/2022/formulas/mathematics/college/ncvj7gbnoftbozcozwhp7oidjwxgf02qxx.png) , so there will always be a
, so there will always be a
![[x]+1](https://img.qammunity.org/2022/formulas/mathematics/college/foikxsaz32qjzb1tziihe24ghmz1hnjj3j.png) . So, we don't need to worry about the domain impacting the range.
. So, we don't need to worry about the domain impacting the range.
![[x]](https://img.qammunity.org/2022/formulas/mathematics/college/ncvj7gbnoftbozcozwhp7oidjwxgf02qxx.png) can be any integer from
can be any integer from
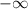 to
to
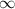 , and as
, and as
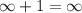 (at least in terms of a function's range and domain), the range of
(at least in terms of a function's range and domain), the range of
![[x]+1](https://img.qammunity.org/2022/formulas/mathematics/college/foikxsaz32qjzb1tziihe24ghmz1hnjj3j.png) is equal to the range of
is equal to the range of
![[x]](https://img.qammunity.org/2022/formulas/mathematics/college/ncvj7gbnoftbozcozwhp7oidjwxgf02qxx.png) , which is
, which is
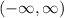 .
.
So, the answer is
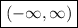 and we're done!
and we're done!