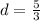Answer:
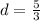
Explanation:
In the slope- intercept form (y= mx +c), the coefficient of x is the slope of the graph.
y= 3x +4
Slope of given line= 3
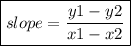
The product of the slopes of perpendicular lines is -1.
![(3)[ (d - 4)/(5 - ( - 2)) ] = - 1](https://img.qammunity.org/2022/formulas/mathematics/college/4rmtko06wdsx930ufpfoouwd72d27kl1vr.png)
Divide both sides by 3:
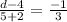
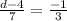
Cross multiply:
3(d -4)= -1(7)
Expand:
3d -12= -7
Add 12 on both sides:
3d= 12 -7
3d= 5
Divide both sides by 3: