Answer:
 can be
can be
 ,
,
 , or
, or

Explanation:
Let's split the inequality and solve it piece by piece.
Case:
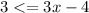
We add
 to both sides to get
to both sides to get
 .
.
We divide both sides by
 to get
to get
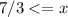 .
.
So,
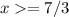 .
.
Case:
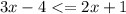
We subtract 2x from both sides to get
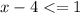 .
.
We add
 to both sides to get
to both sides to get
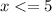 .
.
So, we want to find the integer solutions to
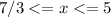 .
.
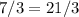 , so
, so
 can be
can be
 ,
,
 , or
, or
 .
.
So,
 can be
can be
 ,
,
 , or
, or
 and we're done!
and we're done!