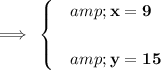Explanation:

The frequency distribution table is as follow

Given that,
- Sum of all frequencies = 100
So,
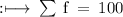
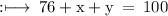
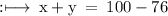
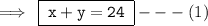
Further given that,
- Median of the series, M = 525
We know, Median is evaluated by using the formula,
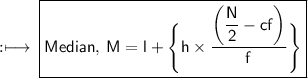
Here,
- l denotes lower limit of median class
- h denotes width of median class
- f denotes frequency of median class
- cf denotes cumulative frequency of the class preceding the median class
- N denotes sum of frequency
According to the given distribution table,
We have
- Median class is 500 - 600
So, we have
By substituting all the given values in the formula,
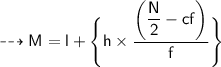
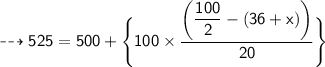
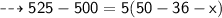
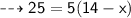
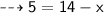
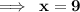
On substituting the value of x in equation (1), we get
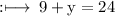
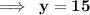
Hence,