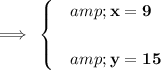Question

The media of the following data is 525. Find the value of x and y, if the total frequency is 100.

Class interval Frequency (fᵢ)
0 - 100 2
100 - 200 5
200 - 300 x
300 - 400 12
400 - 500 17
500 - 600 20
600 - 700 y
700 - 800 9
800 - 900 7
900 - 100 4
​

Answer 1

Explanation:

`\large\underline{\sf{Solution-}}`

The frequency distribution table is as follow

`\begin{gathered}\begin{gathered}\begin{gathered}\boxed{\begin{array}c\sf Class\: interval&\sf Frequency\: (f)&\sf \: cumulative \: frequency\\\frac{\qquad \qquad}{}&\frac{\qquad \qquad}{}\\\sf 0 - 100&\sf 2&\sf2\\\\\sf 100 - 200 &\sf 5&\sf7\\\\\sf 200-300 &\sf x&\sf7 + x\\\\\sf 300-400 &\sf 12&\sf19 + x\\\\\sf 400-500 &\sf 17&\sf36 + x\\\\\sf 500-600 &\sf 20&\sf56 + x\\\\\sf 600-700 &\sf y&\sf56 + x + y\\\\\sf 700 - 800&\sf 9&\sf65 + x + y\\\\\sf 800-900&\sf 7&\sf72 + x + y\\\\\sf 900-1000&\sf 4&\sf76 + x + y\\\frac{\qquad}{}&\frac{\qquad}{}\\\sf & \sf & \end{array}}\end{gathered}\end{gathered}\end{gathered}`

Given that,

• Sum of all frequencies = 100

So,

`\rm :\longmapsto\: \sum \: f \: = \: 100`

`\rm :\longmapsto\: 76 + x + y \: = \: 100`

`\rm :\longmapsto\: x + y \: = \: 100 - 76`

`\rm\implies \:\boxed{ \: \tt{ x + y = 24 \: }} - - - (1)`

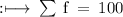
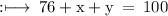
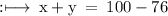
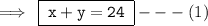
Further given that,

• Median of the series, M = 525

We know, Median is evaluated by using the formula,

`\rm :\longmapsto\:\boxed{ \sf Median, \: M= l + \Bigg \{h * ( \bigg( (N)/(2) - cf \bigg))/(f) \Bigg \}}`

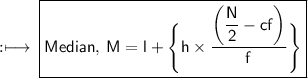
Here,

• l denotes lower limit of median class

• h denotes width of median class

• f denotes frequency of median class

• cf denotes cumulative frequency of the class preceding the median class

• N denotes sum of frequency

According to the given distribution table,

We have

• Median class is 500 - 600

So, we have

• l = 500,

• h = 100,

• f = 20,

• cf = 36 + x

• N = 100

By substituting all the given values in the formula,

`\dashrightarrow\sf M= l + \Bigg \{h * ( \bigg( (N)/(2) - cf \bigg))/(f) \Bigg \}`

`\dashrightarrow\sf 525= 500 + \Bigg \{100 * ( \bigg( (100)/(2) - (36 + x) \bigg))/(20) \Bigg \}`

`\dashrightarrow\sf 525 - 500 = 5(50 - 36 - x)`

`\dashrightarrow\sf 25 = 5(14 - x)`

`\dashrightarrow\sf 5 =14 - x`

`\bf\implies \:x = 9`

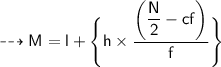
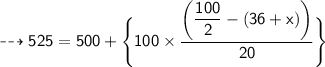
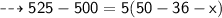
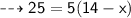
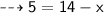
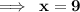
On substituting the value of x in equation (1), we get

`\rm :\longmapsto\:9 + y = 24`

`\bf\implies \:y = 15`

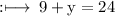
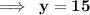
Hence,

`\begin{gathered}\begin{gathered}\bf\: \rm\implies \:\begin{cases} &\bf{x = 9} \\ \\ &\bf{y = 15} \end{cases}\end{gathered}\end{gathered}`