Question

Please help find resultant force of the figure

Answer 1

The resultant force will be 5 N in the South West Direction.

Step-by-step explanation:

Tip:

If we have two vectors A and B, their resultant is:

`\boxed{ \mathsf{Resultant = A^2+B^2+2AB\:cos(\theta)}}`

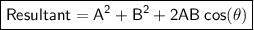
`\theta` is the angle between A and B

Since, Force is a vector quantity, the answer to he given diagram will be thought out by Vector Laws of Addition.

Solution:

6N and 9N are in opposite directions, so their resultant will simply be their difference, and it will be pointing in the direction of the vector with larger magnitude.

= 9 - 6

= 3 N

Now, we have two vectors. one of magnitude 4N pointing towards West and the other of magnitude 3N pointing towards South.

• They're at an angle of 90°. (
  `\theta`=90)
• Their resultant will lie in between the two vectors, 4N and 3N.(The South West Direction).

It's magnitude will be equal to
`\mathsf{\red{ \sqrt{4^(2) +3^(2) } }}`

(as cos90=0, we're left with the sum of the squares of the two vectors)

= 5N

Therefore, the resultant force will be 5N towards the South-West.